Simple Interest (SI)
Simple Interest is calculated only on the principal amount throughout the entire period.
Simple Interest Formula
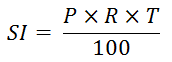
Where:
- SI → Simple Interest
- P → Principal on which interest is calculated
- R → Rate of interest (per annum)
- T → Time (in years)
Amount Formula
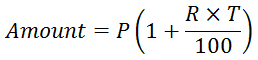
Advanced Simple Interest Formulae
When a sum becomes n times in t years
If a certain sum becomes n times in t years, then rate r is:
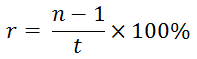
Comparison of Different Rates
If a sum of money at r₁% rate becomes n₁ times of itself in a certain time and becomes n₂ times of itself at r₂% rate in the same period of time, then:
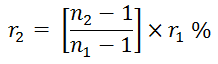
Compound Interest (CI)
Compound interest is interest calculated on the initial principal and also on the accumulated interest of previous periods of a deposit or loan.
Compound Interest Formulae
I. When interest is compounded annually
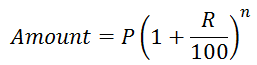
II. When interest is compounded half-yearly
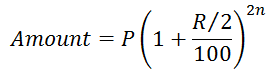
III. When interest is compounded quarterly
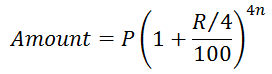
IV. When interest is compounded annually but time is fractional
When time is in fraction, say  years:
years:
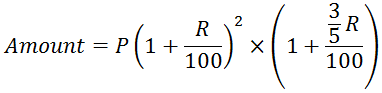
V. Present Worth Formula
Present worth of x due n years is given by:
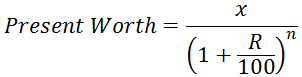
Important Formulae: Difference between CI and SI
If D is the difference between the CI and SI on a sum P at the rate of r%, then:
For Different Time Periods
1. When time is 2 years
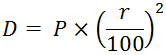
2. When time is 3 years
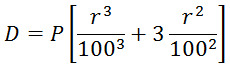
Alternative Formula for 2 Years
If SI is the simple interest and CI is the compound interest on a certain sum P at the rate r% per annum for a time of 2 years, then the difference D between CI and SI is:
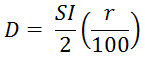
Comparison: Simple Interest vs Compound Interest
Key Differences
Simple Interest
- Interest calculated only on principal
- Interest remains constant each year
- Growth is linear
- Formula: SI = (P × R × T) / 100
- Used in: Short-term loans, simple deposits
Compound Interest
- Interest calculated on principal + accumulated interest
- Interest increases each year
- Growth is exponential
- Formula: A = P(1 + R/100)ⁿ
- Used in: Bank deposits, investments, loans
Problem Solving Tips
Time Calculation Rules
- For counting the time between two given dates, only one of the two dates is counted (either first or last). Usually, we exclude the date of start and include the date of return.
- For converting the time in days into years, always divide by 365, whether it is a leap year or not.
- The time must be taken in accordance with the interest rate percent. Thus, if the interest rate is per month then time must be taken in months.
Quick Calculation Tips
For Simple Interest
- If rate and time are equal, SI is directly proportional to principal
- If principal and time are equal, SI is directly proportional to rate
- If principal and rate are equal, SI is directly proportional to time
For Compound Interest
- Higher compounding frequency = Higher effective interest rate
- For small rates and short time periods, CI ≈ SI
- The difference between CI and SI increases with time and rate
Common Question Types
Type 1: Finding Principal, Rate, or Time
Example: If ₹1000 becomes ₹1200 in 2 years at simple interest, find the rate.
Solution: SI = 1200 - 1000 = ₹200
Using SI = (P × R × T)/100: 200 = (1000 × R × 2)/100
R = 10% per annum
Type 2: Difference between CI and SI
Example: Find the difference between CI and SI on ₹5000 for 2 years at 10% per annum.
Solution: Using D = P(R/100)² for 2 years
D = 5000 × (10/100)² = 5000 × 0.01 = ₹50
Type 3: Population/Depreciation Problems
Example: A city's population grows at 5% per annum. If current population is 100,000, find population after 3 years.
Solution: A = P(1 + R/100)ⁿ
A = 100,000(1 + 5/100)³ = 100,000(1.05)³ = 115,762