HCF (Highest Common Factor)
It is also known as GCD (Greatest Common Divisor) and GCF (Greatest Common Factor). The HCF of two or more numbers is the largest of their common factors.
Example:
- Factors of 10 are 1, 2, 5 and 10.
- Factors of 15 are 1, 3, 5 and 15.
- Here, greatest and common factor of 10 and 15 is 5.
- Therefore, their HCF is 5.
Methods of Finding HCF
1. Factorization Method
Express each of the given numbers as the product of their prime factors. The product of least power of common prime factors gives HCF.
Example: Determine the HCF of 36 and 64.
Solution:
- 36 = 2 × 2 × 3 × 3 = 2² × 3²
- 64 = 2 × 2 × 2 × 2 × 2 × 2 = 2⁶
- Here, least powers of prime factors are 2² and 3⁰.
- Therefore, HCF = 2² = 4
2. Division Method
Divide the larger number by the smaller number. Now, divide the divisor by the remainder. Repeat this process until we get zero as remainder. The last divisor is the required HCF.
Example: Determine the HCF of 72 and 48.
Solution:
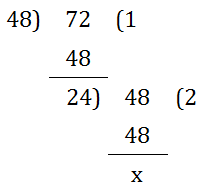
HCF Division Method
Therefore, HCF = 24
LCM (Least Common Multiple)
LCM of two numbers is the smallest number which is a multiple of both the numbers.
Example:
- Multiples of 6 are 6, 12, 18, 24, 30, ...
- Multiples of 4 are 4, 8, 12, 16, 20, 24, ...
- Here, smallest common multiple of 6 and 4 is 12.
- Therefore, their LCM is 12.
Methods of Finding LCM
1. Factorization Method
Express each of the given numbers as the product of their prime factors. The product of all the prime factors of each of the given number with greatest index of common prime factors gives the LCM.
Example: Find the LCM of 72, 108 and 210.
Solution:
- 72 = 2³ × 3²
- 108 = 2² × 3³
- 210 = 2 × 3 × 5 × 7
- Here, highest power of all factors 2³, 3³, 5 and 7.
- Therefore, LCM = 2³ × 3³ × 5 × 7 = 7560
2. Division Method
Arrange the given numbers in a row separating them by commas and divide by a number which divides exactly at least two of the given numbers and write their quotient in the next row. Also, carry down the numbers which are not divisible. Repeat this process till no two of the numbers are divisible by same number except one. The product of the divisors and the undivided number is the required LCM.
Example: Find the LCM of 16, 24, 35 and 42.
Solution:
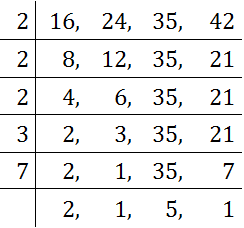
LCM Division Method
Therefore, LCM = 2 × 2 × 2 × 3 × 7 × 2 × 5 = 1680
Important Formulae

Important HCF and LCM Formulae
Key Formulae to Remember:
- HCF × LCM = Product of two numbers
- LCM = (Product of numbers) ÷ HCF
- HCF = (Product of numbers) ÷ LCM
- For three or more numbers: LCM × HCF ≠ Product of numbers
Problem Solving Tips
Type 1: Greatest Number Problems
Question Type:
Find the greatest number that will divide x, y and z exactly.
Tip: The required number is the HCF of x, y and z.
Question Type:
Find the greatest number that will divide x, y and z leaving remainders a, b and c, respectively.
Tip: The required number is the HCF of (x-a), (y-b) and (z-c).
Type 2: Smallest Number Problems
Question Type:
Find the smallest number which is exactly divisible by x, y and z.
Tip: The required number is the LCM of x, y and z.
Question Type:
Find the smallest number which when divided by x, y and z leaves the remainders a, b and c, respectively.
Tip: If a = b = c, then required number = LCM of x, y, z + a
If remainders are different, then required number = LCM of (x-a), (y-b) and (z-c) + a (when x-a = y-b = z-c)
Advanced Applications
Real-Life Applications
- Time and Work: Finding when events will occur together
- Traffic Lights: When different signals will synchronize
- Gear Ratios: In mechanical systems
- Music: Rhythm and beat synchronization
- Astronomy: Planetary alignments and cycles
Special Cases
Co-prime Numbers
When HCF of two numbers is 1, they are called co-prime or relatively prime.
Example: HCF(15, 28) = 1, so 15 and 28 are co-prime.
Property: For co-prime numbers, LCM = Product of the numbers.
When one number divides another
If number a divides number b, then:
- HCF(a, b) = a (smaller number)
- LCM(a, b) = b (larger number)